Here we present the report of three practical applications of the integration of advancing rational fractions:
,
,
.
Calculate the integral:
.
Here, under the sign of the integral, there is a rational function; Steps of the rich member of the standard ( 3 ) is less than the step of the rich term of the numeral ( 4 ). It is necessary for that hand to see the whole part of the fraction.
1.
We see a whole fraction of a fraction. Dilimo x 4
on x 3 - 6 x 2 + 11 x - 6:
Zvіdsi
.
2.
We lay out the banner of the fraction into multipliers. For which it is necessary to expand cubic equalization:
.
6
1, 2, 3, 6, -1, -2, -3, -6
.
Imagine x = 1
:
.
1
. Dilimo x - 1
:
Zvіdsi
.
Virishuemo square equal.
.
Root line:,.
Todi
.
3.
Let's lay it out in simple terms.
.
Father, we knew:
.
Integrable.
Calculate the integral:
.
Here, at the numerator, the fraction is a rich term of the zero step ( 1 = x0). The bannerman has a rich member of the third stage. Oskilki 0 < 3 , then drіb is correct. Let's decompose її on the simplest fractions.
1.
We lay out the banner of the fraction into multipliers. For whom it is necessary to virishiti the third degree:
.
It is acceptable that there may be only one root. Todі vіn є dіlnik number 3
(Member without x). So the whole root can be one of the numbers:
1, 3, -1, -3
.
Imagine x = 1
:
.
Father, we knew one root x = 1
. Dilimo x 3 + 2 x - 3 on x- 1
:
Otzhe,
.
Virishuemo square alignment:
x 2+x+3=0.
Known discriminant: D = 1 2 - 4 3 = -11. Oskilki D< 0
, then there are no real roots. In this rank, we took away the layout of the banner into multipliers:
.
2.
.
(x - 1) (x 2 + x + 3):
(2.1)
.
Imagine x = 1
. Todi x - 1 = 0
,
.
Let's imagine in (2.1)
x= 0
:
1 = 3 A - C;
.
Equal to (2.1)
coefficients at x 2
:
;
0=A+B;
.
.
3.
Integrable.
(2.2)
.
For the calculation of another integral, it is visible in the number book that the banner is gone, and the banner is brought up to the sum of squares.
;
;
.
Calculable I 2
.
.
Oskilki Rivnyannia x 2+x+3=0 do not have real roots, then x 2 + x + 3 > 0. Therefore, the module sign can be omitted.
Supplied in (2.2)
:
.
Calculate the integral:
.
Here, under the sign of the integral, there are drіb іz rich terms. Therefore, the integrated virase is a rational function. Steps of a polynomial in the number book 3 . Steps of the polynomial of the banner of the fraction are more expensive 4 . Oskilki 3 < 4 , then drіb is correct. That її can be laid out in the simplest fractions. Ale for whom it is necessary to lay out a banner on multipliers.
1.
We lay out the banner of the fraction into multipliers. For whom it is necessary to virishiti equal the fourth step:
.
It is acceptable that there may be only one root. Todі vіn є dіlnik number 2
(Member without x). So the whole root can be one of the numbers:
1, 2, -1, -2
.
Imagine x = -1
:
.
Father, we knew one root x = -1
. Dilimo x - (-1) = x + 1:
Otzhe,
.
Now it is necessary to virishiti equalize the third step:
.
How to let go, what is equal to the root of the root, to the number of the dilnik 2
(Member without x). So the whole root can be one of the numbers:
1, 2, -1, -2
.
Imagine x = -1
:
.
Father, we knew one more root x = -1
. It is possible to b, like i in the front slope, add a rich term to, but we can group the terms:
.
Oskilki Rivnyannia x 2 + 2 = 0
do not have real roots, then we took away the layout of the banner into multipliers:
.
2.
Let's lay it out in simple terms. Shukaєmo layout at the sight:
.
Zvіlnyaєmosya vіd znamennik fraction, multiplied by (x + 1) 2 (x 2 + 2):
(3.1)
.
Imagine x = -1
. Todi x + 1 = 0
,
.
Prodifferentially (3.1)
:
;
.
Imagine x = -1
it's crazy that x + 1 = 0
:
;
;
.
Let's imagine in (3.1)
x= 0
:
0 = 2A + 2B + D;
.
Equal to (3.1)
coefficients at x 3
:
;
1=B+C;
.
Father, we knew the layout on the simplest fractions:
.
3.
Integrable.
.
“A mathematician is just like an artist, he sings, he creates vizorunks. And just like that, the vizierunki are bigger than the style, less than the stench of the warehouse of ideas... the idea is just like that, like colors, but the words are guilty, one to one. Beauty is the first help: the world has no space for ugly mathematics».
G.H.Hardi
In the first division, it was planned that it was necessary to understand the first to achieve simple functions, since it was impossible to learn through elementary functions. At the link with cim, these classes of functions are of great practical importance, about which one can say for sure that their first - elementary functions. To such a class of functions can be seen rational functions, which is an expression of two algebraic rich terms Before integrating rational fractions, make a rich task. Therefore, it is important to consider integrating such functions.
Rational fraction(otherwise shot-rational function) is called the extension of two algebraic rich terms:
de i - rich segments.
Guess what rich member (polynomial, whole rational function) n-th stage is called the function of the mind
de 
- decimal numbers. For example,
- a rich member of the first stage;
- rich term of the fourth degree, etc.
Rational drіb (2.1.1) is called correct like a step lower than a step, tobto. n<m, in a different way drіb is called wrong.
If there is any wrong fraction, you can give it to the sight of the sum of a rich member (whole part) and the correct fraction (fractional part). Seeing the whole and the shot parts of an irregular shot can be carried out according to the rule below the rich parts “kut”.
Example 2.1.1. See the number and the shot part of the advancing irregular rational fractions:
A)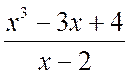 
, b) 
.
Solution . a) Vikoristovuyuchi algorithm rozpodіlu "kutochok", otrimuєmo
In this manner, we take
.
b) Here, too, the vikoristovuєmo algorithm is subdivided into a “kutochok”:
As a result, we take
.
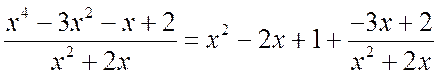Let's bring the bags. The non-values of the integral in the form of a rational fraction in the common fall can be shown by the sum of the integrals in the form of a rich term and in the form of a proper rational fraction. Knowing the primary types of polynomials does not become difficult. To that, they gave me the most important correct rational fractions.
Among the correct rational fractions, they see chotiri tipi, yakі bring up simplest (elementary) rational fractions:
|
3) |
4) |
de - tile number, 
, then. square trinomial 
I don't have real roots.
Integration of the simplest fractions of the 1st and 2nd type does not become great difficulties:
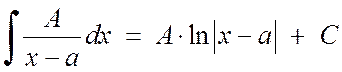, (2.1.3)
. (2.1.4)
We can now look at the integration of the simplest fractions of the 3rd type, and the fractions of the 4th type cannot be seen.
Let's look at the integration
.
The whole integral is counted with the path of seeing the full square in the banner. As a result, the tabular integral of the offensive form
or 
.
Stock 2.1.2. Know the integrals:
A)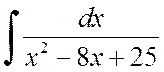 
, b) 
.
Solution . a) It is visible from the square trinomial that the square is:
Zvіdsi know
b) Seeing from the square trinomial the new square, we take:
in such a manner,
.
To know the integral
you can see in the numeral book the denomination of the banner and the spread of the integral at the sum of two integrals: the first one is substantiated 
look up to look
,
and the other - up to a wide-eyed view.
Example 2.1.3. Know the integrals:
.
Solution
. We respect that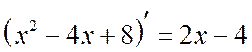 
. We see in the numeral book the banner of the banner:
The first integral is calculated after an additional substitution 
:
Another integral can see the same square at the banner
Remaining, take
Be a correct rational drіb 
can be shown with a single rank in looking at the sum of the simplest fractions. For whom the banner should be laid out in multiples. From the point of view of algebra, it is clear that the skin is a rich term from the effective coefficients
Material, contributions to these topics, spirals on the vіdomosti, filings in the topics "Rational fractions. Arrangement of rational fractions on elementary (simple) fractions". Even the raju would like to quickly glance over this topic before him, as if proceeding to reading this material. In addition, we will need a table of insignificant integrals.
I guess a sprinkling of terms. I talked about them in a separate topic, so here I will mix up short formulas.
The extension of two rich terms $\frac(P_n(x))(Q_m(x))$ is called a rational function or a rational fraction. Rational drіb is called correct Yaxcho $n< m$, т.е. если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе. В противном случае (если $n ≥ m$) дробь называется wrong.
Elementary (simplest) rational fractions are called rational fractions of several types:
Note (bazhan for more understanding of the text): show
New needs of mind $p^2-4q< 0$ в дробях третьего и четвертого типов? Рассмотрим квадратное уравнение $x^2+px+q=0$. Дискриминант этого уравнения $D=p^2-4q$. По сути, условие $p^2-4q < 0$ означает, что $D < 0$. Если $D < 0$, то уравнение $x^2+px+q=0$ не имеет действительных корней. Т.е. выражение $x^2+px+q$ неразложимо на множители. Именно эта неразложимость нас и интересует.
For example, for expression $x^2+5x+10$ it is possible to take: $p^2-4q=5^2-4\cdot 10=-15$. Oskіlki $p^2-4q=-15< 0$, то выражение $x^2+5x+10$ нельзя разложить на множители.
Before speech, for cієї reverification, it is not obov'yazykovo, so the coefficient before $x^2$ is 1. For example, for $5x^2+7x-3=0$ it is necessary: $D=7^2-4\cdot 5 \cdot (-3) = $109. If $D > 0$, then $5x^2+7x-3$ can be multiplied.
Apply rational fractions (correct and incorrect), and you can also know how to apply a rational fraction on elementary fractions. Here we are left with less food for their integration. Let's start with the integration of elementary fractions. Also, it is not easy to integrate the skins of several types of the most important elementary fractions, victorious formulas, shown below. I'm guessing that $n=2,3,4,ldots$ is transferred to type (2) and (4) integrating fractions. Formulas (3) and (4) mean $p^2-4q< 0$.
\begin(equation) \int \frac(A)(x-a) dx=A\cdot \ln |x-a|+C \end(equation) \begin(equation) \int\frac(A)((x-a)^n )dx=-\frac(A)((n-1)(x-a)^(n-1))+C \end(equation) \begin(equation) \int \frac(Mx+N)(x^2 +px+q) dx= \frac(M)(2)\cdot \ln (x^2+px+q)+\frac(2N-Mp)(\sqrt(4q-p^2))\arctg\ frac(2x+p)(\sqrt(4q-p^2))+C \end(equation)
For $\int\frac(Mx+N)((x^2+px+q)^n)dx$ replace $t=x+\frac(p)(2)$, after subtraction the interval is divided into two. The first one is counted after the additional introduced n_d differential sign, and the other one looks like $I_n=\int\frac(dt)((t^2+a^2)^n)$. The goal integral is to take on the help of recurrent spiving
\begin(equation) I_(n+1)=\frac(1)(2na^2)\frac(t)((t^2+a^2)^n)+\frac(2n-1)(2na ^2)I_n, \; n\in N \end(equation)
The calculation of such an integral is analyzed on butt No. 7 (div. third).
There is a higher algorithm for integrating rational fractions that can not be transversely good - universal wine. Tobto. with the help of this algorithm it is possible to integrate be-yaku rational drib. For the very same reason, all the replacements for the undefined integral (Euler's, Chebishev's substitutions, the universal trigonometric substitution) can be swarmed with such a rozrachunk, so that after replacing the rational drib. And before it already zasosuvat algorithm. Bezperedn є zastosuvannya tsgogo algorithm rasberem on butts, beforehand zrobivsh small primіku.
$$ \int\frac(7dx)(x+9)=7\ln|x+9|+C. $$
It is not easy to take the integral from the principle without a mechanical formula. If you blame the constant $7$ for the sign of the integral and guess that $dx=d(x+9)$, then you can take:
$$ \int\frac(7dx)(x+9)=7\cdot \int\frac(dx)(x+9)=7\cdot \int\frac(d(x+9))(x+9 )=|u=x+9|=7\cdot\int\frac(du)(u)=7\ln|u|+C=7\ln|x+9|+C. $$
For detailed information, I recommend looking at the topic. There it is reportedly explained how such integrals are violated. To the point of speech, the formula is brought up by the very same transformations, which were stopped at this point at the hour of the ceremony "manually".
2) I’m going to start two ways: stop the formula ready, or do without it. How to stop the formula , next check which coefficient before $x$ (number 4) can be cleaned up. For this qiu, the fourth is simply guilty of the temples:
$$ \int\frac(11dx)((4x+19)^8)=\int\frac(11dx)(\left(4\left(x+\frac(19)(4)\right)\right)^ 8)= \int\frac(11dx)(4^8\left(x+\frac(19)(4)\right)^8)=\int\frac(\frac(11)(4^8)dx) (\left(x+\frac(19)(4)\right)^8). $$
Now it's time to fill in the formula:
$$ \int\frac(\frac(11)(4^8)dx)(\left(x+\frac(19)(4)\right)^8)=-\frac(\frac(11)(4 ^8))((8-1)\left(x+\frac(19)(4) \right)^(8-1))+C= -\frac(\frac(11)(4^8)) (7\left(x+\frac(19)(4) \right)^7)+C=-\frac(11)(7\cdot 4^8 \left(x+\frac(19)(4) \right )^7)+C. $$
You can get around and zastosuvannya formulas. І navit without fault of the constant $4$ for the arms. If you don't mind that $dx=\frac(1)(4)d(4x+19)$, then you can take:
$$ \int\frac(11dx)((4x+19)^8)=11\int\frac(dx)((4x+19)^8)=\frac(11)(4)\int\frac( d(4x+19))((4x+19)^8)=|u=4x+19|=\\ =\frac(11)(4)\int\frac(du)(u^8)=\ frac(11)(4)\int u^(-8)\;du=\frac(11)(4)\cdot\frac(u^(-8+1))(-8+1)+C= \\ =\frac(11)(4)\cdot\frac(u^(-7))(-7)+C=-\frac(11)(28)\cdot\frac(1)(u^7 )+C=-\frac(11)(28(4x+19)^7)+C. $$
Detailed explanations about the meaning of similar integrals are given in the topic "Integrating with a setting (introducing a sign of a differential)".
3) We need to integrate $\frac(4x+7)(x^2+10x+34)$. This drib takes the structure $\frac(Mx+N)(x^2+px+q)$, de $M=4$, $N=7$, $p=10$, $q=34$. However, in order to perekonatisya, sho dіysno elementary drіb of the third type, it is necessary to revіrt vikonannya um $p^2-4q< 0$. Так как $p^2-4q=10^2-4\cdot 34=-16 < 0$, то мы действительно имеем дело с интегрированием элементарной дроби третьего типа. Как и в предыдущих пунктах есть два пути для нахождения $\int\frac{4x+7}{x^2+10x+34}dx$. Первый путь - банально использовать формулу . Подставив в неё $M=4$, $N=7$, $p=10$, $q=34$ получим:
$$ \int\frac(4x+7)(x^2+10x+34)dx = \frac(4)(2)\cdot \ln (x^2+10x+34)+\frac(2\cdot 7-4\cdot 10)(\sqrt(4\cdot 34-10^2)) \arctg\frac(2x+10)(\sqrt(4\cdot 34-10^2))+C=\\ = 2\cdot \ln (x^2+10x+34)+\frac(-26)(\sqrt(36)) \arctg\frac(2x+10)(\sqrt(36))+C =2\cdot \ln (x^2+10x+34)+\frac(-26)(6) \arctg\frac(2x+10)(6)+C=\\ =2\cdot \ln (x^2+10x +34)-\frac(13)(3) \arctg\frac(x+5)(3)+C. $$
Virishimo this butt, but without using the ready-made formula. Let's try to see the bannerman in the numeral book. What does it mean? We know that $(x^2+10x+34)"=2x+10$. We need to include $2x+10$ in the number book itself. For now, the number book is only worth $4x+7$, but not for long. Zastosuєmo to the numeral such a transformation:
$$ 4x+7=2cdot 2x+7=2cdot (2x+10-10)+7=2cdot(2x+10)-2cdot 10+7=2cdot(2x+10) -13. $$
Now the numerator has got the necessary amount $2x+10$. And our integral can be rewritten in such a way:
$$ \int\frac(4x+7)(x^2+10x+34) dx= \int\frac(2xcdot(2x+10)-13)(x^2+10x+34)dx. $$
Rosіb'єmo pіdіntegralny drіb for two. Well, apparently, the integral itself is "separated":
$$ \int\frac(2\cdot(2x+10)-13)(x^2+10x+34)dx=\int \left(\frac(2\cdot(2x+10)))(x^ 2 +10x+34)-\frac(13)(x^2+10x+34) \right)\; dx=\\ =\int \frac(2\cdot(2x+10))(x^2+10x+34)dx-\int\frac(13dx)(x^2+10x+34)=2\cdot \int \frac((2x+10)dx)(x^2+10x+34)-13cdot\int\frac(dx)(x^2+10x+34). $$
Let's talk about the first integral, tobto. about $\int \frac((2x+10)dx)(x^2+10x+34)$. Oskіlki $d(x^2+10x+34)=(x^2+10x+34)"dx=(2x+10)dx$, then in the number book of the integrand fraction, the denominator differential is expanded. +10)dx$ can be written $d(x^2+10x+34)$.
Now let's say a couple of words about another integral. You can see the new square in the banner: $ x 2 + 10 x + 34 = (x + 5) 2 + 9 $. In addition, $dx=d(x+5)$ is wrong. Now, the sum of integrals, which we have previously taken away, can be rewritten in a different way:
$$ 2\cdot\int \frac((2x+10)dx)(x^2+10x+34)-13\cdot\int\frac(dx)(x^2+10x+34) =2\cdot \int \frac(d(x^2+10x+34))(x^2+10x+34)-13cdot\int\frac(d(x+5))((x+5)^2+ 9) . $$
If I replace $u=x^2+10x+34$ in the first integral, then in the future I will look at $\int\frac(du)(u)$ and just take another formula z . As far as the other integral is concerned, then for the new one the replacement $u=x+5$ is changed, if I see $\int\frac(du)(u^2+9)$ in the future. This pure water is eleven formulas from tables of insignificant integrals. Otzhe, turning to the sum of the integrals, matimemo:
$$ 2\cdot\int \frac(d(x^2+10x+34))(x^2+10x+34)-13\cdot\int\frac(d(x+5))((x+ 5 )^2+9) =2cdotln(x^2+10x+34)-frac(13)(3)arctgfrac(x+5)(3)+C. $$
We took away the very evidence that, even when the formulas are stuck, it’s not surprising, well. Vzagalі, the formula is brought in the same ways, yakі mi vikoristovuvali for the value of the integral. I respect that a respected reader can blame one food here, I’ll formulate yogo for that:
Catering №1
To add the integral $\int \frac(d(x^2+10x+34))(x^2+10x+34)$ to another formula from the tables of non-trivial integrals, we should take the following:
$$ \int \frac(d(x^2+10x+34))(x^2+10x+34)=|u=x^2+10x+34|=\int\frac(du)(u) =\ln|u|+C=\ln|x^2+10x+34|+C. $$
Why does the solution have a daily module?
Notice to request No. 1
Nutrition is a regular law. The modulus is less than that which is equal to $x^2+10x+34$ for any $x\in R$ greater than zero. Tsezovsіm clumsily show kіlkom with paths. For example, $x^2+10x+34=(x+5)^2+9$ and $(x+5)^2 ≥ 0$, then $(x+5)^2+9 > 0$ . You can judge otherwise, without losing sight of the entire square. Shards $10^2-4\cdot 34=-16< 0$, то $x^2+10x+34 >0$ for whatever $x\in R$ (which is why this logical lancet calls out, the graphic method of arranging square irregularities will surprise you). In the skin case, $x^2+10x+34 > 0$, then $|x^2+10x+34|=x^2+10x+34$, then. The replacement of the module can be replaced by variable arches.
Mustache butt No. 1 was omitted;
Vidpovid:
Butt #2
Find the integral $\int\frac(7x+12)(3x^2-5x-2)dx$.
At first glance, the integrand $\frac(7x+12)(3x^2-5x-2)$ is already similar to the elementary drib of the third type, that is. to $\frac(Mx+N)(x^2+px+q)$. It turns out that the only difference is the coefficient of $3$ before $x^2$, but the coefficient and clean up the bad (for the bows). However, the similarity exists. For the fraction $\frac(Mx+N)(x^2+px+q)$ obov'zkovoy є Umov $p^2-4q< 0$, которое гарантирует, что знаменатель $x^2+px+q$ нельзя разложить на множители. Проверим, как обстоит дело с разложением на множители у знаменателя нашей дроби, т.е. у многочлена $3x^2-5x-2$.
We have a coefficient in front of $x^2$ is not more equal to one, so check with my mind $p^2-4q< 0$ напрямую мы не можем. Однако тут нужно вспомнить, откуда взялось выражение $p^2-4q$. Это всего лишь дискриминант квадратного уравнения $x^2+px+q=0$. Если дискриминант меньше нуля, то выражение $x^2+px+q$ на множители не разложишь. Вычислим дискриминант многочлена $3x^2-5x-2$, расположенного в знаменателе нашей дроби: $D=(-5)^2-4\cdot 3\cdot(-2)=49$. Итак, $D >0$, then $3x^2-5x-2$ can be multiplied by $3x^2-5x-2$. And it means that $\frac(7x+12)(3x^2-5x-2)$ is not an elementary fraction of the third type, and it stops to the integral $\int\frac(7x+12)(3x^2- 5x-2)dx$ formula is not possible.
Well, if the tasks of rational fractions are not elementary, then it is necessary to give a sum of elementary fractions, and then integrate them. Shorter seeming, slower. How to lay out a rational drib on an elementary report is written. Let’s look at the fact that the banner is laid out on multipliers:
$$ 3x^2-5x-2=0;\\ \begin(aligned) & D=(-5)^2-4\cdot 3\cdot(-2)=49;\\ & x_1=\frac( -(-5)-sqrt(49))(2cdot 3)=frac(5-7)(6)=frac(-2)(6)=-frac(1)(3); \\ & x_2=\frac(-(-5)+\sqrt(49))(2\cdot 3)=\frac(5+7)(6)=\frac(12)(6)=2. \\end(aligned)\\ 3x^2-5x-2=3\cdot\left(x-\left(-\frac(1)(3)\right)\right)\cdot (x-2)= 3cdotleft(x+frac(1)(3)right)(x-2). $$
The subinternal drіb can be represented in the following way:
$$ \frac(7x+12)(3x^2-5x-2)=\frac(7x+12)(3\cdot\left(x+\frac(1)(3)\right)(x-2) )=\frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2)). $$
Now we can expand $\frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2))$ into elementary:
$$ \frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2)) =\frac(A)(x+\frac( 1)(3))+\frac(B)(x-2)=\frac(A(x-2)+B\left(x+\frac(1)(3)\right))(\left(x+ ) \frac(1)(3)\right)(x-2));\\\frac(7)(3)x+4=A(x-2)+B\left(x+\frac(1) ( 3)\right). $$
To know the coefficients $A$ and $B$, there are two standard ways: the method of insignificant coefficients and the method of substituting private values. Let's create a method for substituting private values, substituting $x=2$, and then $x=-\frac(1)(3)$:
$$ \frac(7)(3)x+4=A(x-2)+B\left(x+\frac(1)(3)\right).\x=2;\; \frac(7)(3)\cdot 2+4=A(2-2)+B\left(2+\frac(1)(3)\right); \; \frac(26)(3)=\frac(7)(3)B;\; B=\frac(26)(7).\x=-\frac(1)(3);\; \frac(7)(3)\cdot \left(-\frac(1)(3) \right)+4=A\left(-\frac(1)(3)-2\right)+B\left (-\frac(1)(3)+\frac(1)(3)\right); \; \frac(29)(9)=-\frac(7)(3)A;\; A=-\frac(29\cdot 3)(9\cdot 7)=-\frac(29)(21).\\ $$
Oskіlki koefіtsіenti found, left out of writing down the ready layout:
$$ \frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2))=\frac(-\frac(29)( 21))(x+frac(1)(3))+frac(frac(26)(7))(x-2). $$
In principle, you can leave out such a record, but I’ll change to the soul a neat option:
$$ \frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2))=-\frac(29)(21)\ cdotfrac(1)(x+frac(1)(3))+frac(26)(7)cdotfrac(1)(x-2). $$
Turning to the outer integral, we can imagine up to a new otriman layout. Potim rozіb'єmo іtegral for two, and until the skin zastosuєmo formula. Constantly, I will be guilty for the sign of the integral:
$$ \int\frac(7x+12)(3x^2-5x-2)dx =\int\left(-\frac(29)(21)\cdot\frac(1)(x+\frac(1) (3))+\frac(26)(7)\cdot\frac(1)(x-2)\right)dx=\\ =\int\left(-\frac(29)(21)\cdot\ frac(1)(x+\frac(1)(3))\right)dx+\int\left(\frac(26)(7)\cdot\frac(1)(x-2)\right)dx =- \frac(29)(21)\cdot\int\frac(dx)(x+\frac(1)(3))+\frac(26)(7)\cdot\int\frac(dx)(x-2 )dx=\\ =-\frac(29)(21)\cdot\ln\left|x+\frac(1)(3)\right|+\frac(26)(7)\cdot\ln|x- 2|+C. $$
Vidpovid: $\int\frac(7x+12)(3x^2-5x-2)dx=-\frac(29)(21)\cdot\ln\left|x+\frac(1)(3)\right| + frac (26) (7) cdot ln | x-2 | +C$.
Butt #3
Find the integral $\int\frac(x^2-38x+157)((x-1)(x+4)(x-9))dx$.
We need to integrate $\frac(x^2-38x+157)((x-1)(x+4)(x-9))$. The number one has a polynomial of another level, and the standard one has a polynomial of the third level. The shards of the steps of a polynomial for a numeralist are less than the steps of a polynomial for a bannerman, tobto. $2< 3$, то подынтегральная дробь является правильной. Разложение этой дроби на элементарные (простейшие) было получено в примере №3 на странице, посвящённой разложению рациональных дробей на элементарные. Полученное разложение таково:
$$ \frac(x^2-38x+157)((x-1)(x+4)(x-9))=-\frac(3)(x-1)+\frac(5)(x +4)-frac(1)(x-9). $$
We will be left with less tasks to solve the integral for three, and to suffocate the formula to the skin. Constantly, I will be guilty for the sign of the integral:
$$ \int\frac(x^2-38x+157)((x-1)(x+4)(x-9))dx=\int\left(-\frac(3)(x-1) +\frac(5)(x+4)-\frac(1)(x-9) \right)dx=\=-3\cdot\int\frac(dx)(x-1)+ 5\cdot \ int\frac(dx)(x+4)-\int\frac(dx)(x-9)=-3\ln|x-1|+5\ln|x+4|-\ln|x- 9 |+C. $$
Vidpovid: $\int\frac(x^2-38x+157)((x-1)(x+4)(x-9))dx=-3\ln|x-1|+5\ln|x+ 4 |-\ln|x-9|+C$.
Prodovzhennya analysis of applications for those roztashovane in another part.
We continue to work on the integration of fractions. Integrals of certain types of fractions have already been looked at in lessons, and this lesson in the singing sense can be continued. For a successful understanding of the material, the basic skills of integration are necessary, so that you have already started to develop integrations, then with a teapot, then it is necessary to start these statistics Integr. Apply solution .
It’s not surprising, at the same time we’re busy not so much with the importance of integrations, like ... with systems linear rivers. In zvyazku z cym nonchalantly I recommend that you learn the lesson And for yourself - it is necessary to be kindly oriented in the methods of installation (the "school" method and the method of member-by-member folding (revision) of the system).
What is a fractional-rational function? In simple words, shot-rational function - ce drіb, at the numerator and bannerman, they change rich terms and create polynomials. With which fractions є twisted, lower tі, about yakі it was said in the article Integration of real fractions .
In addition, an example and a typical algorithm for deriving an integral as a fractional-rational function.
butt 1
Krok 1. First of all, we need to work with the integral in the form of a fractional-rational function - ce z'yasovuєmo foot food: chi є drіb correct? This krok is victorious, and at once I will explain how:
On the back we marvel at the number book and z'yasovuemo senior step rich member: 
The senior step of the numeral book is older than two.
Now marveling at the banner that z'yasovuёmo senior step banner. Asking for a way - rozkriti bows and bring similar dodanki, but you can do it simpler, skin duzhtsі know the senior step 
and thoughts are multiplied: - in this rank, the senior step of the bannerman is three. It is quite obvious that if you really open the arms, then we do not take a step more than three.
Visnovok: Major step of the numeral STRICTLY less than the senior level of the banner, later, more correct.
Yakby in this butt in the number book contained a rich term 3, 4, 5 and so on. step, then drib buv bi wrong.
Now we can see less of the correct shot-rational functions. Vipadok, if the step of the numeral is greater or more expensive than the step of the banner, we can analyze it like a lesson.
Krok 2 Let's spread the banner into multipliers. We marvel at our banner: 
Seemingly, there are already a lot of multipliers, ale, we are not less, we ask ourselves: why can’t you spread it? The object of the tortur, without a cross, is a quadratic trinomial. Virishuemo square alignment: 
The discriminant greater than zero, then, the trinomial is effectively divided into multipliers:
Rule of thumb: EVERYTHING that can be multiplied by the bannerman can be multiplied
We begin to draw up a decision:
Krok 3 Using the method of non-significant coefficients, we decompose the integrand function into the sum of simple (elementary) fractions. Ninі will be wiser.
Looking at our integrand function: 
And, you know, it seems like an intuitive thought that it would be wrong to turn our great drib into small sprats. For example, the axis is: 
Blame food, but what can you do so? Zіtkhnemo z polegshennyam, vіdpovіdna theorem of mathematical analysis stverdzhuє - POSSIBLE. Such layout is clear and single.
Only one zakovika, coefficients mi Booway I don't know what the name of the method of unimportant coefficients was.
As you have guessed, come on the body so, don't shout! will be directed at those who are schob їх їх DIZNATISYA - z'yasuvati, why are you equal.
Be respectful, I will explain once!
Otzhe, we begin to dance like: 
At the left part, we point the viraz to the sleeping banner:
Now we are safely escaping from the bannermen (because the stench is the same):
In the left part of the curve, the arches are open, there are no coefficients for which it is not yet clear:
At the same time, we repeat the school rule for the multiplication of rich terms. At my hour as a teacher, I learned to follow the rule with stone faces: In order to multiply rich member on rich member it is necessary to multiply the skin member of one rich member by the skin member of another rich member.
From the point of view of a sensible explanation, it is better to bring the coefficients into the bows (want to especially I don’t bother with the method of saving an hour):
We create a system of linear lines.
Back to the top of the senior steps:
І write down the relevant coefficients for the first equal system:
Kindly remember the offensive nuance. What would be b, yakby at the right part of the fire did not bulo? Let's say, it would be beautiful just without a square? And here the equal system would have to put a zero on the right: . Why zero? And to the one in the right part, you can always assign the square with zero: If in the right part of the day, if you change or (i) the variable term, then in the right parts of the second equals of the system, we put zero.
We record the different coefficients of another system: 
I, zreshtoyu, mineral water, pick up free limbs.
Eh, ... I'm on fire. Jarti get out - mathematics is a serious science. In our institute group, no one laughed when the assistant professor said that she was throwing members around number line and choose your best. Nalashtovuєmos in a serious way. Wanting to, who lived to the end of the lesson, all the same will quietly laugh.
System ready:
We repair the system: 
(1) From the first level, it can be shown and represented by the 2nd and 3rd levels of the system. You can really speak (or in a different letter) from the second river, but in this case you can see it yourself from the 1st river, the shards are there least coefficients.
(2) We give similar dodanki to the 2nd and 3rd equals.
3
(4) Substitute for a friend (or third) equal, it is known that
(5) Submit and first equal, otrimuyuchi.
Yakshcho vynikli difficulties with the methods of the system's development How to untie the system of linear lines?
After perfecting the system, start a thorough re-verification - present the known values at the skin equalization of the system, as a result, everything can settle down.
Mayzha arrived. The coefficients are known, moreover: 
A neatly designed task can look something like this:
Yak bachite, the main problem of the task was to put together (correctly!) and fold (correctly!) the system of linear alignments. And at the final stage, everything is not so smooth: the victorious power of the linearity of the undefined integral is integrable. I’m sorry that under the skin of the three integrations we have a “free” collapsible function, about the peculiarities of integration I’m growing The method of replacing the change in an undefined integral .
Revision: Differentiation:
We have removed the pidintegral function, but the integral was found correctly.
In the course of the re-verification, I had a chance to hang up to a sleeping banner, but it didn’t turn out badly. The method of non-significant coefficients and bringing it to the bottom of the banner is mutually beneficial.
butt 2
Know the non-values of the integral. 
Let's turn to the fraction from the first butt: 
. It doesn’t matter to remember that all the multipliers of RIZNI are in the banner. Blame nutrition, but what work, like a tribute, for example, such a drіb: 
? Here at the banner we have a step, otherwise, mathematically multiples. In addition, there is a quadratic trinomial that cannot be multiplied 
negative, we can’t divide it into multipliers of trinomials). What work? The layout of the sum of elementary fractions looks like a kshtalt 
with unknown coefficients in the mountains, as if otherwise?
butt 3
Show function 
Krok 1. Verify that we have the right drib
The senior step of the number dial: 2
The senior step of the banner: 8
Otzhe, drіb є correct.
Krok 2 Can you lay it out at the bannerman for multipliers? It is obvious that not everything is laid out already. The square trinomial does not expand in the world for other reasons. Good. Robots are less.
Krok 3 Let's give a shot-rational function to look at the sum of elementary fractions.
In this view, the arrangement may look like this:
We marvel at our banner:
When spreading the shot-rational function on the sum of elementary fractions, three important points can be mentioned:
1) If there is a “self-made” multiplier in the banner at the first step (at our point of view), then we put the non-insignificance coefficient on the top (at our point of view). Applied No. 1,2 were formed less of such "lonely" multipliers.
2) Yakshcho at the bannerman є multiple multiplier, then it is necessary to arrange it like this: 
- so sequentially go through all the steps of the "iks" from the first to the last step. Our butt has two multiples: take another look at the layout I have laid out and change, that the stink of the layout itself follows this rule.
3) If the banner knows a non-expandable polynomial of another level (y razі), then when arranging in the number book, it is necessary to write down a linear function with non-significant coefficients (y razі z non-significant coefficients i).
Actually, it’s still the 4th turn, but I’ll stop talking about the new one, the shards in practice are rarely seen.
butt 4
Show function 
at the sight of the sum of elementary fractions from the unknown coefficients.
This is an example of an independent solution. Outwardly, the solution is that it is similar to the lesson.
Be careful with the algorithm!
If you have sorted out, according to some principles, you need to put a shot rational function into a bag, then you can practically draw out any kind of integral of the type that you are looking at.
butt 5
Know the non-values of the integral. 
Krok 1. It is obvious that drіb є is correct:
Krok 2 Can you lay it out at the bannerman for multipliers? It's possible, it's possible. Here is the sum of cubes 
. We spread the banner into multipliers, vikoristovuyuchi the formula of the fast multiplier
Krok 3 Using the method of non-significant coefficients, we decompose the integrand function into the sum of elementary fractions:
To take into account that the rich term is not divisible into multipliers (reverse, that the discriminant is negative), then we put a linear function with unknown coefficients, and not just one letter.
We direct the drіb to the sleeping banner:
We store and install the system:
(1) From the first level, it can be compared and presented on another level of the system (the most rational way).
(2) We induce similar dodanki from another equal.
(3) We add term by term to each other and the third equal system.
The mustache is farther away, the system is clumsy in principle, usnі, oskіlki. 
(1) We write down the sum of the fractions in a reasonable way to the known coefficients.
(2) Vykoristuemo power of the linearity of the undefined integral. What happened to the other integral? With this method, you can find out in the rest of the lesson Integration of real fractions .
(3) Once again, the victorious power of linearity. At the third integral, we begin to see the second square (remote paragraph to the lesson Integration of real fractions ).
(4) We take another integral, for the third one we see the same square.
(5) We take the third integral. Ready.
,
,
